-
핀홀카메라 모델, 동차좌표, 카메라 캘리브레이션Image Geometry 2021. 7. 27. 16:04
이 섹션의 함수는 소위 핀홀 카메라로 불리는 모델을 사용합니다. 장면의 뷰는 대응하는 픽셀 p를 형성하는 원근변환(perspective transformation)을 사용하여, 한 장면의 3D 포인트 Pw에서 이미지 평면으로의 투영(projecting)에 의해 얻어집니다. Pw와 p 는 모두 동차좌표(homogeneous coordinates)로 표현됩니다. 즉, 3D와 2D 동차벡터(homogeneous vector)로 각각으로 표현됩니다. 투영기하(projective geometry), 동차벡터(homogeneous vector) 그리고 동차변환(homogeneous transformations)에 대한 간략한 소개를 이 섹션의 소개 끝부분에서 찾아볼 수 있습니다. 보다 더 간결한 표기법을 위하여, 우리는 종종 동차벡터 대신 "동차"를 제거하고 벡터라고 말합니다.
핀홀 카메라 모델에 의해 주어지는 왜곡없는 투영 변환(distortion-free projective transformatin)은 아래에 보여집니다.
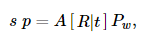
여기서 Pw 는 월드좌표계(world coordinate system)에 대해 표현된 하나의 3D포인트 이고, p는 이미지평면의 하나의 2D 픽셀, A는 카메라 내부행렬(Intrinsic matrix), R와 t는 월드에서 카메라 좌표계(camera coordinate system, or camera frame)로의 좌표 변경을 설명하는 회전(rotation)과 이동(translation)이고, s는 투영 변환의 임의의 스케일링이며 카메라 모델이고 카메라 모델의 일부는 아닙니다.
카메라 내부행렬 A ([293]에서 사용되고 일반적으로 K로 사용표기)는 카메라 좌표계(camera coordinates system)에 주어진 3D포인트들을 2D픽셀 좌표로 투영합니다.

카메라 내부행렬 A는 픽셀단위(pixel units)로 표시되는 초점거리fx와 fy, 그리고 일반적으로 이미지 중심에 가까운 주점(cx, cy)으로 구성됩니다.
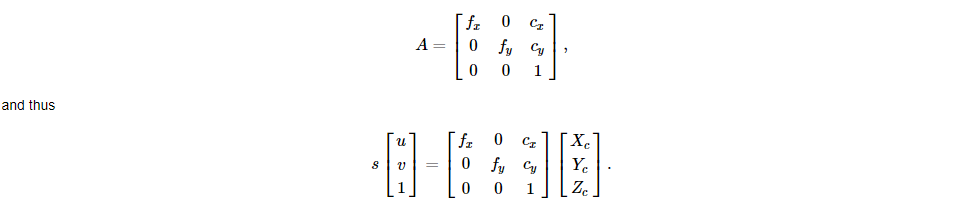
내부 매개변수의 행렬(the matrix of intrinsic parameters)은 장면뷰에 따라 달라지지 않습니다. 따라서 한 번 추정되면, 초점거리(focal length)가 고정되어 있는 한(줌 렌즈의 경우) 재사용 할 수 있습니다. 그러므로 만약 카메라의 한 이미지가 한 요소에 의해 스케일된다면, 이런 모든 매개변수들은 동일한 요소로 스케일(각각에 대해 곱셈/나눗셈) 되어야할 필요가 있습니다.
회전-이동 행렬 [ R | t ]는 투영변환(projective transformation)과 동차변환(homogeneous transformation)의 행렬곱입니다. 3x4 투영변환(projective transformation) 카메라 좌표로 표시된 3D포인트들을 이미지 평면의 2D포인트들로 맵핑하고, 정규화된 카메라 좌표로 표시합니다.

동차 변환(homogeneous transformation)은 외부매개변수 R과 t에의해 인코드 되고, 월드좌표계(world coordinate system) w에서 카메라좌표계(camera coordinate system) c로의 기저변화(change of basis)를 표현한다. 그러므로, 월드 좌표 Pw에서 점 P가 주어지면 다음과 같이 카메라좌표계 Pc에서 P의 표현을 얻을 수 있다.
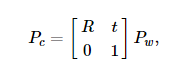
이 동차변환은 3x3회전 행렬과 3x1 이동 벡터 t로 구성됩니다.

투영변환(projective transformation)과 동차변환(homogeneous transformation)을 결합하여, 우리는 월드 좌표계의 3D포인트들을 정규화된 카메라 좌표(normalized camera coordinates)와 이미지 평면의 2D포인트로 맵핑하는 투영변환(projective transformation)을 얻습니다.
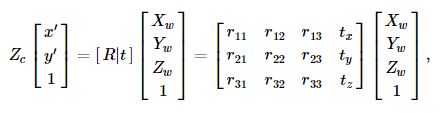
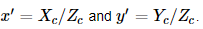
내부(intrinsic)와 외부(extrinsic)에 대한 방정식을 함께 쓰면, 다음과 같이 표기되며

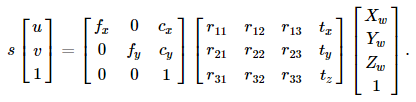
만약 Zc != 0 이면, 위의 변환은 다음과 동일합니다.

아래의 그림은 핀홀 카메라 모델을 나타냅니다.
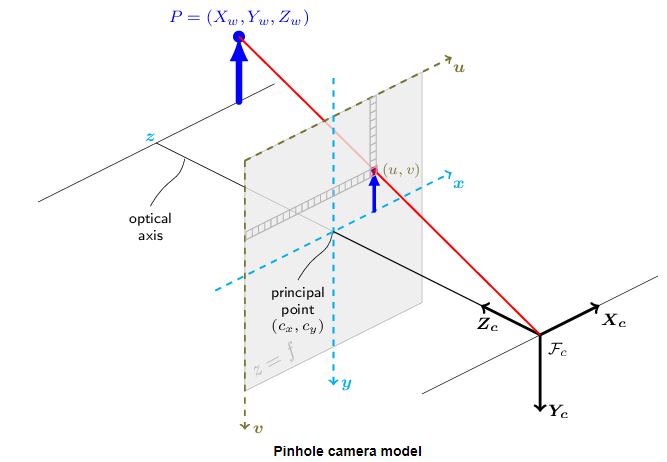
실제 렌즈들은 일반적으로 약간의 왜곡, 대부분 방사왜곡(radial distortion)이고 약간의 접선왜곡(tangential distortion)을 가집니다. 따라서 위의 모델은 다음과 같이 확장됩니다.

왜곡 매개변수(distortion parameters)는 방사계수(radial coefficients) k1, k2, k3, k4, k5, k6이고, p1와 p2는 접선왜곡 계수(tangential distortion coefficients)이고, s1, s2, s3, s4 든 얇은 프리즘 왜곡 계수(thin prism distortion coefficients)입니다. Higher-order는 OpenCV에서 고려되지 않습니다.
다음 그림은 방사형 왜곡의 두 가지 일반타입을 보여줍니다:
방사왜곡은 실제 렌즈에 대해 항상 단조(monotonic)이며, 만약 추정기가 비-단조 결과를 생성하면, 캘리브레이션 실패로 고려해야 합니다. 더 일반적으로, 방사왜곡은 반드시 단조(monotonic)이고 왜곡 함수는 반드시 전단사(bijective)여야 합니다. 실패된 추정결과는 이미지의 센터 근처에서 믿을 수 없을 정도로 좋아보일 수 있지만, AR/SFM 등의 응용프로그램에서 비정상적으로 수행될 것입니다. OpenCV 카메라 캘리브레이션에서 사용되는 최적화 방법에서, 프레임워크는 필요한 정수 프로그래밍(integer programming)과 다항 부등식(polynomial inequalities)을 지원하지 않으므로, 이러한 제약을 포함하지 않습니다. 추가적인 정보는 이슈#15992에서 확인할 수 있습니다.

어떤 경우, 이미지 센서가 카메라 앞의 비스듬한평면에 초점을 맞추기위해 기울어질 수 있습니다(Scheimpflug 이론). 이는 입자 이미지 유속계(particle image velocimetry, PIV) 또는 레이저팬을 사용하는 삼각화(triangulation)에 유용할 수 있습니다. 기울기는 x" 와 y"의 원근왜곡(perspective distortion)의 원인입니다. 이 왜곡은 다음과 같이 모델링 될 수 있습니다[152].

즉, 만약 벡터가 4개의 요소를 포함하면, k3=0 임을 의미합니다. 왜곡계수(distortion coefficients)는 장면의 뷰에 따라 달라지지 않습니다. 그러므로 그들은 또한 내부 카메라 매개변수(intrinsic camera parameters)에 속합니다. 그리고 캡처된 이미지 해상도에 관계없이 동일하게 유지됩니다. 예를들어, 한 카메라가 320x240해상도의 이미지에 대해 캘리브레이션 된 경우, 완벽하게 동일한 왜곡 계수가 같은 카메라의 640 x 480 이미지에 대해 사용될 수 있지만, fx, fy, cx, cy 는 적절하게 조정되어야 합니다.
아래의 함수는 위의 모델을 사용하여 다음을 실행합니다.
- 3D포인트들을 내부, 외부 매개변수가 주어진 이미지 평면에 투영합니다.
- 적은수의 3D포인트, 그리고 그 투영, 내부매개변수가 주어지면 외부 매개변수를 계산합니다.
- 여러개의 알려진 캘리브레이션 패턴의 뷰에서 내부, 외부 카메라 매개변수를 추정합니다. (모든 뷰는 여러개의 3D-2D포인트 대응으로 설명됩니다.)
- 스테레오카메라 "헤드"의 상대적인 포지션과 방향을 추정하고 카메라 광축을 평행하게 만드는 rectification 변환을 계산합니다.
동차좌표(homogeneous Coordinates)
동차좌표는 투영기하(projective geometry)에서 사용되는 좌표계(a system of coordinates)입니다. 그것을 사용하면 무한에서의 포인트들을 유한좌표로 표현할 수 있으며, 카르테시안(cartesian) 대응(counterparts)와 비교할 때 수식을 단순화합니다. 예를들어, 어파인 변환(affine transformation)이 선형 동차 변환(linear homogeneous transformation)으로 표현될 수 있다는 장점을 가집니다.
n-차원 카르테시안 벡터(cartesian vector) P를 따라 1을 덧붙여서 동차벡터(homogeneous vector) Ph를 얻습니다. 예를들어, P->Ph로 맵핑하는 3D 카르테시안 벡터(cartesian vector)는 다음과 같습니다.
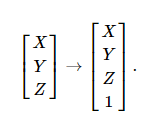
역 맵핑 Ph->P의 경우, 동차벡터(homogeneous vector)의 모든 요소(elements)를 마지막 요소로 나눕니다. 예를들어 3D동차벡터의 경우 2D 카르테시안 대응을 다음과 같이 얻습니다. W는 0이 아니어야 합니다.

이 맵핑으로 인해, k != 0인, 한 개의 동차 포인트의 모든 배수 kPh 는 동일한 포인트 Ph를 표현한다. 이 속성의 직관적인 이해는 투영변환(projectove transformation)에서는 Ph의 모든 배수들이 동일한 포인트에 맵핑된다는 것입니다. 이것은 카메라의 핀홀을 통과하는 한 광선을 따르는 모든 점들은 동일한 이미지 포인트에 투영되기 때문에, 핀홀카메라에 대해 수행되는 물리적 관찰입니다. 예를들어, 위의 핀홀 카메라모델의 이미지에서 빨간색 광선에 속한 모든 점들은 동일한 이미지 좌표에 맵핑됩니다. 이 속성은 또한 핀홀 카메라모델의 방정식에서 스케일 모호성 s 에 대한 소스입니다.
언급한 바와 같이, 동차 좌표를 사용하여, 우리는 R과 t에 의해 매개변수화(parameterized) 된 기준(basis)의 any 변화를선형변환으로써 표현할 수 있습니다. 예를들면, 좌표계(coordinate system) 0에서 좌표계 1로의 기준(basis) 변경은 다음과 같습니다.
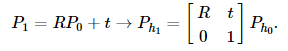
Note
- 이 모듈의 다양한 함수는 카메라 내부 행렬을 입력 매개변수로 취합니다. 비록 모든 함수가 이 매개변수의 동일한 구조를 가정하지만, 그것들의 이름은 다르게 지어져있을 수 있습니다. 그러나, 매개변수의 설명은 카메라 내부 행렬 명확해질 것입니다.
- 수평 위치에서의 카메라 3대에 대한 캘리브레이션 샘플은 opencv_source_code/samples/cpp/3calibration.cpp
- 일련의 이미지들에 기반한 캘리브레이션 샘플은 opencv_source_code/samples/cpp/calibration.cpp
- 3D 재구성을 위한 캘리브레이션 샘플은 opencv_source_code/samples/cpp/build3dmodel.cpp
- 스테레오 캘리브레이션에 대한 캘리브레이션 예제는 opencv_source_code/samples/cpp/stereo_calib.cpp
- 스테레오 매칭에 대한 캘리브레이션 예제는 opencv_source_code/samples/cpp/stereo_match.cpp
- (파이썬) 캘리브레이션 샘플은 opencv_source_code/samples/python/calibrate.py
Reference
[1] https://docs.opencv.org/4.5.2/d9/d0c/group__calib3d.html#gad3fc9a0c82b08df034234979960b778c